位运算实验(上)
Data Lab: Manipulating Bits #1 - 对于实验一(Data Lab)的一些想法(上)。
这个实验要求学生实现简单的逻辑和算术运算函数,但是只能使用一个非常有限的C语言子集。比如,只能用位级操作来计算一个数字的绝对值。这个实验可帮助学生了解 C语言数据类型的位级表示,以及数据操作的位级行为。
Puzzle 1 - isAsciiDigit
isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters ‘0’ to ‘9’)
Examples: isAsciiDigit(0x35) = 1
isAsciiDigit(0x3a) = 0
isAsciiDigit(0x05) = 0
Legal ops: ! ~ & ^ | + << >>
Max ops: 15
Rating: 3
本题应首先判断参数x是否介于0x30与0x39之间,但实验要求不可使用if等语句,应该考虑位运算的方法。
我们知道,参数x介于0x30与0x39之间,等价于x - 0x30的结果为非负,且x - 0x3a的结果为负。从而可以利用正数与负数的符号位的区别进行进一步运算。
同时注意实验要求不可使用减法运算符,可以用“取反加一”的方法代替之。
1 | int isAsciiDigit(int x) |
Puzzle 2 - anyEvenBit
anyEvenBit - return 1 if any even-numbered bit in word set to 1
Examples: anyEvenBit(0xA) = 0, anyEvenBit(0xE) = 1
Legal ops: ! ~ & ^ | + << >>
Max ops: 12
Rating: 2
本题需要对参数x的偶数位进行判断,故可以利用偶数位全为1、奇数位全为0的“模版”辅助判断。
注意实验要求使用的常数应保证在0~255之间,故可以多次左移来将模版扩大为需要的长度。
同时注意要求中的any even-numbered bit in word set to 1意为只要存在某一偶数位为1即可,并非要求所有偶数位全部为1。所以其反义为“所有偶数位全为0”。
1 | int anyEvenBit(int x) |
Puzzle 3 - copyLSB
copyLSB - set all bits of result to least significant bit of x
Examples: copyLSB(5) = 0xFFFFFFFF, copyLSB(6) = 0x00000000
Legal ops: ! ~ & ^ | + << >>
Max ops: 5
Rating: 2
本题可以利用算术右移时高位填充与符号位有关的特点来解。
1 | int copyLSB(int x) |
Puzzle 4 - leastBitPos
leastBitPos - return a mask that marks the position of the least significant 1 bit. If x == 0, return 0
Example: leastBitPos(0x60) = 0x20
Legal ops: ! ~ & ^ | + << >>
Max ops: 6
Rating: 2
一个数的编码中,“1”所在的位权最小的位的低位全为0,即为“…100…0”的形式(记作1)。按位取反,变为“…011…1”的形式(记作2),再加1得到“…100…0”的形式(记作3)。其中形式3中的“1”的高位与形式2的对应位相同,即与形式1(原数)相反。
形式3即原数的相反数,故可以将参数x与其相反数按位与,较高位均变为0,只保留了“1”所在位权最小位。
1 | int leastBitPos(int x) |
Puzzle 5 - divpwr2
divpwr2 - Compute x/(2^n), for 0 <= n <= 30
Round toward zero
Examples: divpwr2(15,1) = 7, divpwr2(-33,4) = -2
Legal ops: ! ~ & ^ | + << >>
Max ops: 15
Rating: 2
首先可能想到直接对参数x进行右移,但注意右移为算术右移,负数的右移可能会得到错误的结果。
负数除以$2^n$,可以看作它的相反数除以$2^n$后再取相反数。取相反数即“取反加一”,也就是说,当参数x < 0时,x / $2^n$ 与~((~x + 1) >> n) + 1等价。基于此,下面讨论一下此表达式具体的算法。
前提x < 0。首先计算(~x + 1) >> n,不难看出结果与~x的低n位有密切联系,而~x由x按位取反而来,有以下两种情况:
- 当
x的低n位全部为0时,~x运算后的低n位全部变为1,再加1即“等价于”(对较高位来说)在第n位加1(整体加上1 << n),故~x + 1的第n位至第31位(认为最低位为第0位,下同)与~x + (1 << n))的相同。则~((~x + 1) >> n) + 1 = ~((~x + (1 << n)) >> n) + 1 = ~(~x >> n + 1) + 1,此即~x >> n + 1的相反数。而~(~x >> n) + 1为~x >> n的相反数,即满足~(~x >> n) + 1 + ~x >> n = 0,故所求~x >> n + 1的相反数为~(~x >> n),即x >> n。 - 当
x的低n位不全为0时,即至少某一位为1,~x运算后该位变成0,其他位为1,再加1后的进位一定进到了最低的0上,而不会影响到较高位。故~x + 1的第n位至第31位与~x的相同。则~((~x + 1) >> n) + 1 = ~(~x >> n) + 1 = (x >> n) + 1。
可以看出,当x为负数时,只有低n位不全为0时才需要加1。
1 | int divpwr2(int x, int n) |
Puzzle 6 - bitCount
bitCount - returns count of number of 1’s in word
Examples: bitCount(5) = 2, bitCount(7) = 3
Legal ops: ! ~ & ^ | + << >>
Max ops: 40
Rating: 4
查找“1”一共有多少位,首先可能想到按照每一位进行查找,但此时运算符总数会超出上限。所以我们可以把参数x划分为8部分,用“模版”0001 0001 0001 0001 0001 0001 0001 0001来比较,并比较4次。
获得模版的方法同Puzzle 2。
设比较的结果为sum,比较完成之后可以发现,我们已经把参数x的8部分中各自“1”的总数存放在了sum对应的$1/8$部分中,然后将这8部分进行3次“对折”,即可将8部分各自总数加到一起。
1 | int bitCount(int x) |
Puzzle …
同时也要注意代码的规范问题,利用辅助工具可以协助提高代码的质量。
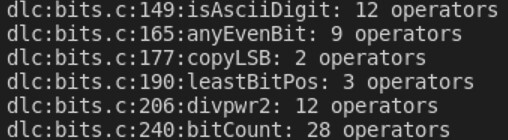
例如,运行./btest以检查函数功能的正确性:
运行./dlc -e bits.c以检查每个函数的运算符使用情况:
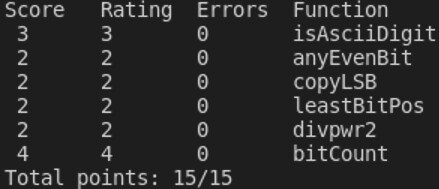
运行./driver.pl以同时输出dlc和BDD checker的结果: